在Python中,通过数据结构来保存项目中重要的数据信息。Python语言内置了多种数据结构,例如列表,元组,字典和集合等。本堂课我们来讲一讲Python中举足轻重的一大数据结构——元组。
在Python中,我们可以将元组看作一种特殊的列表。它与列表唯一的不同在于:元组内的数据元素不能发生改变【这个不变——不但不能改变其中的数据项,而且也不能添加和删除数据项!】。当我们需要创建一组不可改变的数据时,通常是将这些数据放进元组中~
在Python中,创建元组的基本形式是以小括号“()”将数据元素括起来,各个元素之间用逗号“,”隔开。
如下:
tuple1 = ('xiaoming', 'xiaohong', 18, 21)
tuple2 = (1, 2, 3, 4, 5)
# 而且——是可以创建空元组哦!
tuple3 = ()
# 小注意——如果你创建的元组只包含一个元素时,也不要忘记在元素后面加上逗号。让其识别为一个元组:
tuple4 = (22, )
元组和字符串以及列表类似,索引都是从0开始,并且可以进行截取和组合等操作。
如下:
tuple1 = ('xiaoming', 'xiaohong', 18, 21)
tuple2 = (1, 2, 3, 4, 5)
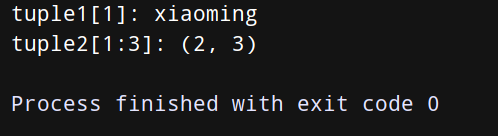
# 显示元组中索引为1的元素的值
print("tuple1[1]:", tuple1[0])
# 显示元组中索引从1到3的元素的值
print("tuple2[1:3]:", tuple2[1:3])
虽然在开头就说元组不可变,但是它还是有个被支持的骚操作——元组之间进行连接组合:
tuple1 = ('xiaoming', 'xiaohong', 18, 21)
tuple2 = (1, 2, 3, 4, 5)
tuple_new = tuple1 + tuple2
print(tuple_new)

虽然元组不可变,但是却可以通过del语句删除整个元组。
如下:
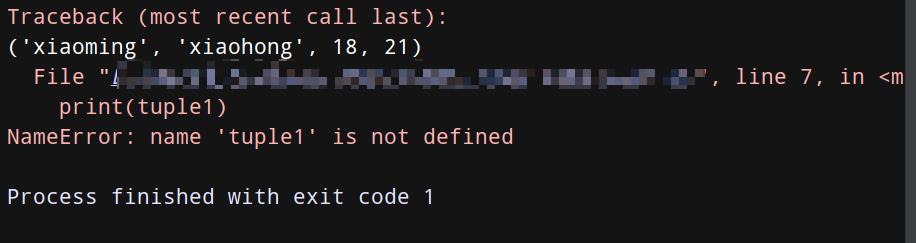
tuple1 = ('xiaoming', 'xiaohong', 18, 21)
print(tuple1) # 正常打印tuple1
del tuple1
print(tuple1) # 因为上面删除了tuple1,所以再打印会报错哦!
元组是不可变,但是我们可以通过使用内置方法来操作元组。常用的内置方法如下:
其实更多时候,我们是将元组先转换为列表,操作之后再转换为元组(因为列表具有很多方法~)。
(1)
Python允许将一个包含N个元素的元组或序列分别为N个单独的变量。这是因为Python语法允许任何序列/可迭代对象通过简单的赋值操作分解为单独的变量,唯一的要求是变量的总数和结构要与序列相吻合。
如下:
tuple1 = (18, 22) x, y = tuple1 print(x) print(y) tuple2 = ['xiaoming', 33, 19.8, (2012, 1, 11)] name, age, level, date = tuple2 print(name) print(date)

如果要分解未知或任意长度的可迭代对象,上述分解操作岂不直接很nice!通常在这类可迭代对象中会有一些已知的组件或模式(例如:元素1之后的所有内容都是电话号码),利用“*”星号表达式分解可迭代对象后,使得开发者能轻松利用这些模式,而无须在可迭代对象中做复杂操作就能得到相关的元素。
在Python中,星号表达式在迭代一个变长的元组序列时十分有用。如下演示分解一个待标记元组序列的过程。
records = [
('AAA', 1, 2),
('BBB', 'hello'),
('CCC', 5, 3)
]
def do_foo(x, y):
print('AAA', x, y)
def do_bar(s):
print('BBB', s)
for tag, *args in records:
if tag == 'AAA':
do_foo(*args)
elif tag == 'BBB':
do_bar(*args)
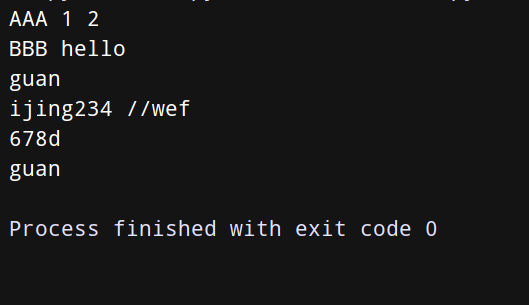
line = 'guan:ijing234://wef:678d:guan'
uname, *fields, homedir, sh = line.split(':')
print(uname)
print(*fields)
print(homedir)
print(sh)
(2)
在Python中迭代处理列表或元组等序列时,有时需要统计最后几项记录以实现历史记录统计功能。
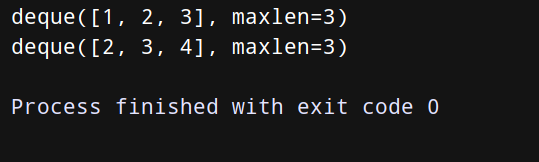
使用内置的deque实现:
from _collections import deque q = deque(maxlen=3) q.append(1) q.append(2) q.append(3) print(q) q.append(4) print(q)
如下——演示了将序列中的最后几项作为历史记录的过程。
from _collections import deque
def search(lines, pattern, history=5):
previous_lines = deque(maxlen=history)
for line in lines:
if pattern in line:
yield line, previous_lines
previous_lines.append(line)
# Example use on a file
if __name__ == '__main__':
with open('123.txt') as f:
for line, prevlines in search(f, 'python', 5):
for pline in prevlines: # 包含python的行
print(pline) # print (pline, end='')
# 打印最后检查过的N行文本
print(line) # print (pline, end='')
123.txt:
pythonpythonpythonpythonpythonpythonpython
python
python
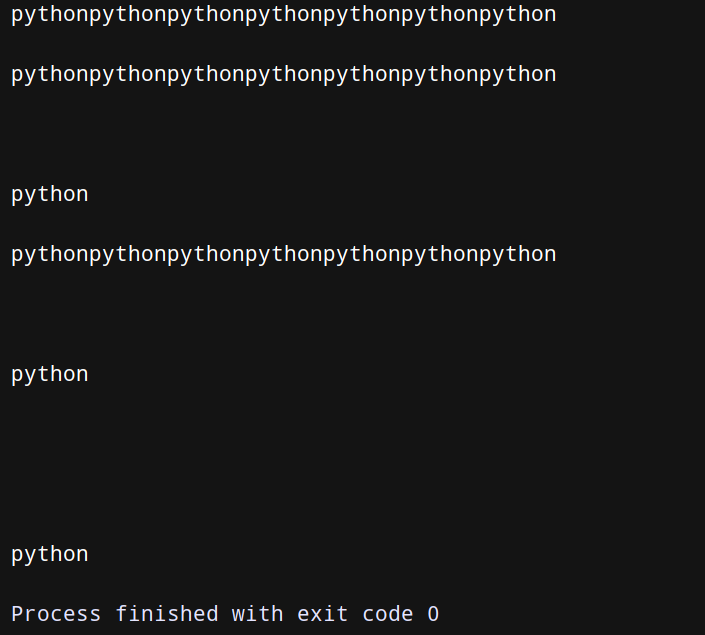
在上述代码中,对一系列文本行实现了简单的文本匹配操作,当发现有合适的匹配时,就输出当前的匹配行以及最后检查过的N行文本。使用deque(maxlen=N)创建了一个固定长度的队列。当有新记录加入而使得队列变成已满状态时,会自动移除最老的那条记录。当编写搜索某项记录的代码时,通常会用到含有yield关键字的生成器函数,它能够将处理搜索过程的代码和使用搜索结果的代码成功解耦开来。
使用内置模块heapq可以实现一个简单的优先级队列。
如下——演示了实现一个简单的优先级队列的过程。
import heapq
class PriorityQueue:
def __init__(self):
self._queue = []
self._index = 0
def push(self, item, priority):
heapq.heappush(self._queue, (-priority, self._index, item))
self._index += 1
def pop(self):
return heapq.heappop(self._queue)[-1]
class Item:
def __init__(self, name):
self.name = name
def __repr__(self):
return 'Item({!r})'.format(self.name)
q = PriorityQueue()
q.push(Item('AAA'), 1)
q.push(Item('BBB'), 4)
q.push(Item('CCC'), 5)
q.push(Item('DDD'), 1)
print(q.pop())
print(q.pop())
print(q.pop())
在上述代码中,利用heapq模块实现了一个简单的优先级队列,第一次执行pop()操作时返回的元素具有最高的优先级。
拥有相同优先级的两个元素(foo和grok)返回的顺序,同插入到队列时的顺序相同。
函数heapq.heappush()和heapq.heappop()分别实现了列表_queue中元素的插入和移除操作,并且保证列表中的第一个元素的优先级最低。
函数heappop()总是返回“最小”的元素,并且因为push和pop操作的复杂度都是O(log2N),其中N代表堆中元素的数量,因此就算N的值很大,这些操作的效率也非常高。
上述代码中的队列以元组 (-priority, index, item)的形式组成,priority取负值是为了让队列能够按元素的优先级从高到底排列。这和正常的堆排列顺序相反,一般情况下,堆是按从小到大的顺序进行排序的。变量index的作用是将具有相同优先级的元素以适当的顺序排列,通过维护一个不断递增的索引,元素将以它们加入队列时的顺序排列。但是当index在对具有相同优先级的元素间进行比较操作,同样扮演一个重要的角色。
在Python中,如果以元组(priority, item)的形式存储元素,只要它们的优先级不同,它们就可以进行比较。但是如果两个元组的优先级相同,在进行比较操作时会失败。这时可以考虑引入一个额外的索引值,以(priority, index, item)的方式建立元组,因为没有哪两个元组会有相同的index值,所以这样就可以完全避免上述问题。一旦比较操作的结果可以确定,Python就不会再去比较剩下的元组元素了。
如下——演示了实现一个简单的优先级队列的过程:
import heapq
class PriorityQueue:
def __init__(self):
self._queue = []
self._index = 0
def push(self, item, priority):
heapq.heappush(self._queue, (-priority, self._index, item))
self._index += 1
def pop(self):
return heapq.heappop(self._queue)[-1]
class Item:
def __init__(self, name):
self.name = name
def __repr__(self):
return 'Item({!r})'.format(self.name)
# ①
a = Item('AAA')
b = Item('BBB')
#a < b 错误
a = (1, Item('AAA'))
b = (5, Item('BBB'))
print(a < b)
c = (1, Item('CCC'))
#② a < c 错误
# ③
a = (1, 0, Item('AAA'))
b = (5, 1, Item('BBB'))
c = (1, 2, Item('CCC'))
print(a < b)
# ④
print(a < c)
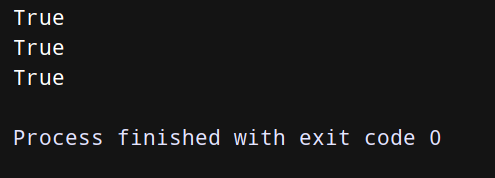
在上述代码中,因为在①~②中没有添加所以,所以当两个元组的优先级相同时会出错;而在③~④中添加了索引,这样就不会出错了!