## 前言
面试中,经常会问到有关于MYSQL 索引的相关概念,我们之前也都学过有关树的概念、以及二叉树、二叉查找树、红黑树等。这一节,来关注经常是数据库索引中使用的B-树
在说这些之前,我们需要了解时间复杂度以及空间复杂度。
## 时间复杂度
时间复杂度,用于鉴定一个算法的好坏、很多时候,比如跑一个for 循环一个数组排序,有冒泡、二分法等方法。相比于冒泡。二分法很占优势,为什么呢?因为比较的次数少、并且做的无用功少、所以这个算法就好。
时间复杂度就是为了表示一个频繁度,这个频繁度怎么说呢。就是每执行一次循环,这就是一个频繁。
`O(频度)` 用O大写字符O表示,而不是零。
常见时间复杂度依次从小到大:
1. O(1) 常数阶
2. O(logn) 对数阶
3. O(n) 线性阶
4. O(n的平方) 平方阶
5. O(n的立方) 立方阶
6. O(2的n次方) (指数阶)
## 空间复杂度
空间复杂度,一般指占用的内存
## 时间换空间、空间换时间
这两个完全是可以等价交换的。比如我们想用
`消耗时间长、换取占用空间少` 这样会使应用程序响应变慢。但是占用内存少
`消耗大量空间、换取快速的响应` 例子:谷歌浏览器
## B-树
切记,这里不念做`B减数` 这里的横岗没有任何意思,就是B树。
来说这个问题之前,首先了解一下:有关索引的简单内容。
我们都知道,索引,就是储存在本地磁盘上的一块数据结构,通过索引,我们能够快速查找数据库指定数据所在的位置。因为需要快速的查找出来。所以性能需要好的数据结构;例如:
1. 二叉查找树 时间复杂度 O(logN)
一般情况下,二叉查找树以二分法查找,时间能够大大减少、一般遍历的最多次数就是二叉树的层级高度。
我们在上面已经了解过有关时间换空间、空间换时间的概念了。所以数据库的索引必须让其快起来,那就必须使用空间去换取时间,一般的索引库都是很大的。几个G甚至更多。
一般情况下,这么大的索引,我们没办法一次性读入到内存中。必须逐一加载的内存当中才可以。
因为是磁盘,就会有读取和写入(IO),使用二叉树虽然性能很高,但是不得不考虑磁盘的IO性能。
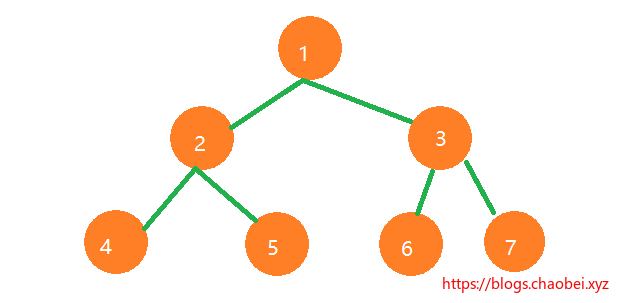
假设在使用二叉树来实现索引。我们查找的数字是`7` 最坏的情况下。也需要读取3次才可找到这个数字,那么有没有情况,就是把这个树的层级减少一些,我们读取的IO次数也就能减少。性能也就能提升。B-树就出来了
### 概念
将原来`瘦高`的二叉树变为`矮胖`的B-树。
B树是一种多路平衡查找树。每一个节点最多包含K个孩子,而K又被称为是B树的阶。这个阶取决于磁盘页大小。
### 特点
假设这个磁盘决定的`B树阶为m`
1. 根节点至少有两个子女。
2. 中间节点都包含(k-1)个元素和K个孩子,其中 `m/2 <= k <= m`
总结上面的话,就是说,这个k 就是节点的元素数量的范围取值范围在于
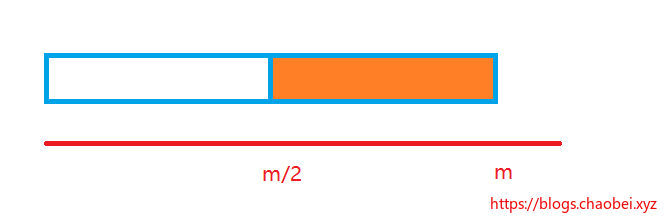
总是不能大于阶,并且也不能少于阶的一半。
3. 每一个叶子节点都包含(k-1)个元素,其中 `m/2 <= k <= m`
4. 所有叶子节点都是位于同一层的
5. 每一个节点的元素从小到大排列,它的第(k-1)个元素正好是其k个孩子所包含元素的值域。(有点难以理解)
### 理解一下
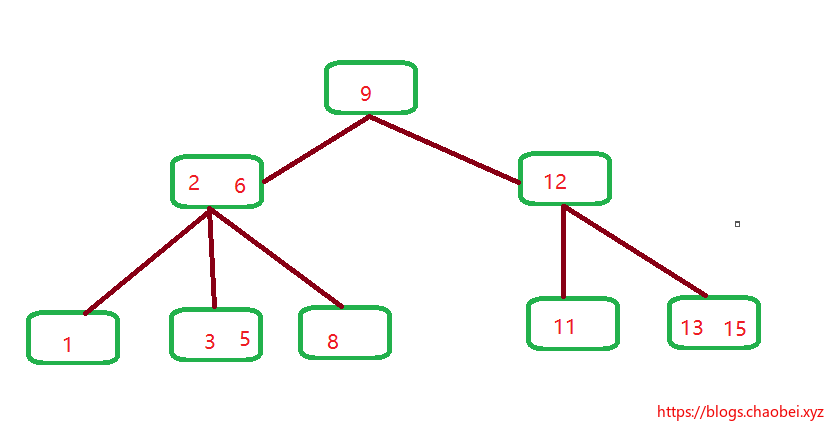
画出一个B树,按照上面的条条框框 我们来说一下:
1. B树根节点`9` 确实有两个子节点
2. 中间的节点都会包含的元素数=子节点数-1。
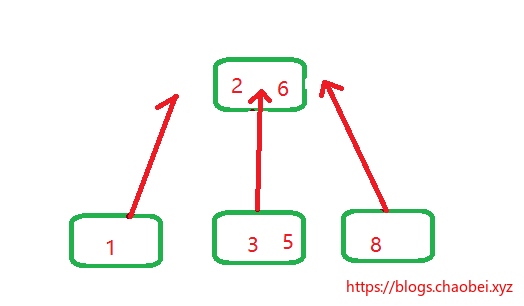
3. 比如`2 6` 这个元素的位置。
我们假设当前的k=2,所以当前节点的k-1=1 第一个元素`2` 正好是第2个子元素`3,5`的值域划分。因为
1. 2 < 3 < 6
2. 2 < 5 < 6
画个图,你就理解了。拿出原来的一小部分,我们来分析
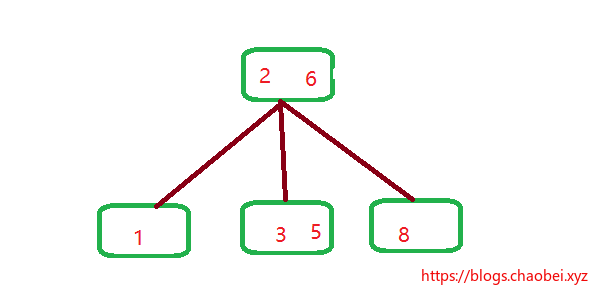
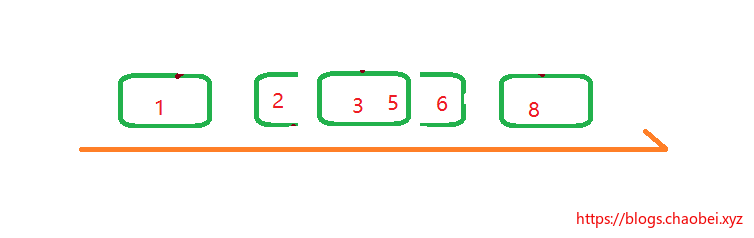
通过箭头的指向,将子元素插入到指定的位置,你会发现什么??
看到了么?变成了一个线性数组,并且已经排序好了的。
## B- 优势
相比于二叉查找树,我们的B-树在缩短与硬盘的交互次数IO ,提升性能。每次只需要读取一个节点,通过本节点在内存中的交互,即可通过值域的方式确定当前的值在那个节点下,依次找寻即可。
## B-树 插入元素
假设我们插入一个`4`,通过遍历,我们发现,必须要插入到这个位置:
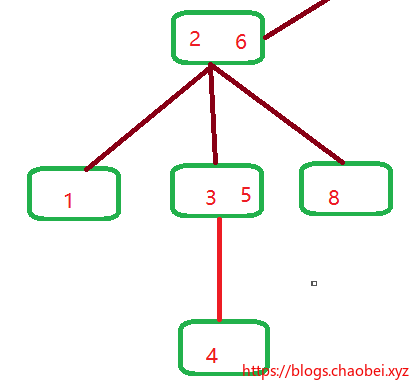
若这样插入,其实是违反规则的,因为父节点`3,5`有两个元素,所以它应该有三个儿子节点才对,所以这样行不通,需要改变!
往上方观察,`2,6` 已经是满节点的状态,并且根节点最多包含两个节点,那只能在根节点入手了。

就需要拆分节点和发生一系列的改变,其实还是很繁琐的。
这里只需要了解这个过程即可。不需要钻牛角尖
## B树优势
B树最大的优势就是自平衡
以及始终能够维持多路平衡,能够最大程度减少磁盘的IO次数而达到性能提升
### 应用场景
那就是数据库索引了。以及文件系统。数据库这里常见的就是MongoDB 一款非关系型数据库。
而我们常用的Mysql数据库则用的是B+树作为索引的。我们下来说一说。
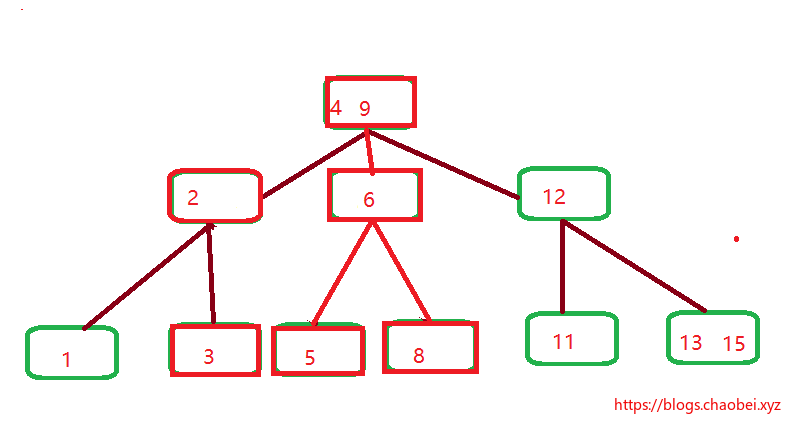
## B+树
所谓B+树,其实就是B树的Plus版本,更加牛皮,所以牛皮在哪儿呢?那无非就是查询性能上,查询快呗。
既然是B树的一种扩展,那么肯定的,也包含B树该有的性质它都有,B+树有的一些性质,我们这里罗列一下:
### 特征
假设这里存在一个m阶的B+树,
1. 有K个子节点的中间节点包含有K个元素,(B树这里是k-1),中间节点的元素不保存数据,只用来索引,所有的数据都保存在叶子节点。
2. 所有的叶子节点包含了全部的元素信息,以及指向这些元素的指针。叶子节点本身按照关键词的大小自小而大顺序排列。
3. 所有的中间节点元素都同时存在与子节点中。在子节点元素中是最大或者最小的元素。
是不是很懵逼?懵逼就对了
待会儿我们来解释一下,不要慌
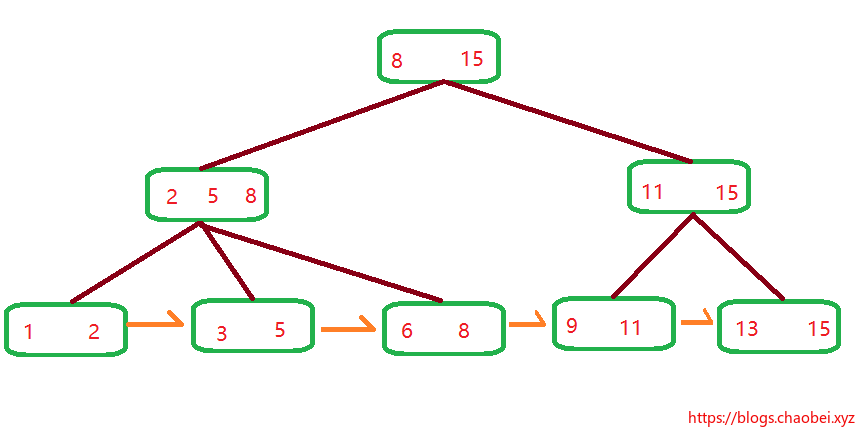
1. 中间节点有三个元素,所以它有三个子节点。没毛病
2. 每个子节点都会包含父节点的一个元素,或者是最大。或者是最小。
3. 它的所有数据都是储存与叶子节点的,并且使用指针指向下一个叶子节点,形成一个`链表`
### 为什么查询性能更优?
我们知道,B树是为了减少磁盘IO而创建出来的,因为二叉树虽然快,但是内存空间有限,一下子读取不了那么多。那就必须按照磁盘页的大小,依次读取节点到内存中。在数据量相同的情况下,因为B树每个节点上都存在数据。而不一样的是,B+树只有在叶子节点才会存在数据,所以呢 同样的情况下,B+树的这种结构,一次性能够放入内存的节点数量就可以增加了。因为B+树中间节点放的是引用地址嘛,这样读取性能又能够翻一翻。
1. 单一节点储存了更多的元素。使得树更加矮胖,读取次数更少
2. 查询都需要到达叶子节点,而后通过链表遍历、更加迅速。
## 小结
总结一下:为了什么发明出B树,因为通过空间换取时间的概念,索引是一个非常庞大的数据结构。而且
`电脑的内存大小有限` 不能一次性把二叉查找树读取进去,只能一点个节点一个节点的读取到里面。内存考虑完了。
`硬盘IO 速度` 因为索引的庞大,所以,在磁盘读取的时候,尽量使用少次的IO读取出我们需要的值,那就是最优解,所以呢,这个二叉树看起来很瘦高,要读取的IO数量太多了。所以呢?
B树就被发明出来了。为了啥?让二叉查找树变得`矮胖`。减少IO次数
B+树呢?作为B树的一个Plus版本。还是由于磁盘页的大小限制,只能读取少量的B树节点到内存中。因为B树节点就带有数据。而B+树就不一样了。因为中间节点不带数据,能够一次性读取好几个节点进去处理。所以呢,性能又提升了!
奥利给!
其实说了这么多,我们可以发现,所有的优化,是建立在当前磁盘不够、IO不够、内存不够大的基础上改善的。
## 参考
https://mp.weixin.qq.com/s/jRZMMONW3QP43dsDKIV9VQ