YOLO v4中用到的激活函数是Mish激活函数
在YOLO v4中被提及的激活函数有: ReLU, Leaky ReLU, PReLU, ReLU6, SELU, Swish, Mish
其中Leaky ReLU, PReLU难以训练,ReLU6转为量化网络设计
激活函数使用过程图:

函数表达式:

Sigmoid函数图像及其导数图像:
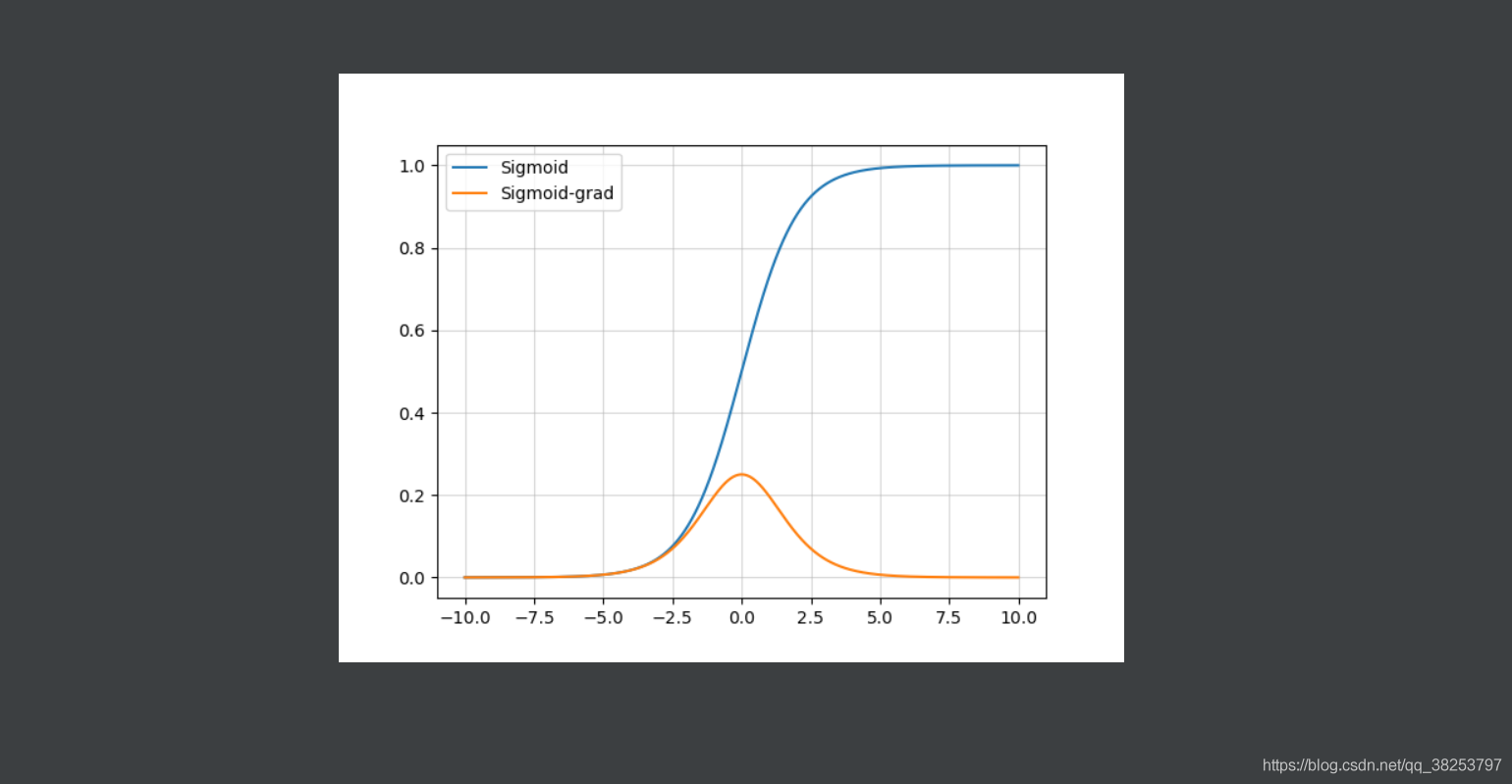
优点:
缺点:
hard-Sigmoid函数时Sigmoid激活函数的分段线性近似。
函数公式:

hard-Sigmoid函数图像和Sigmoid函数图像对比:
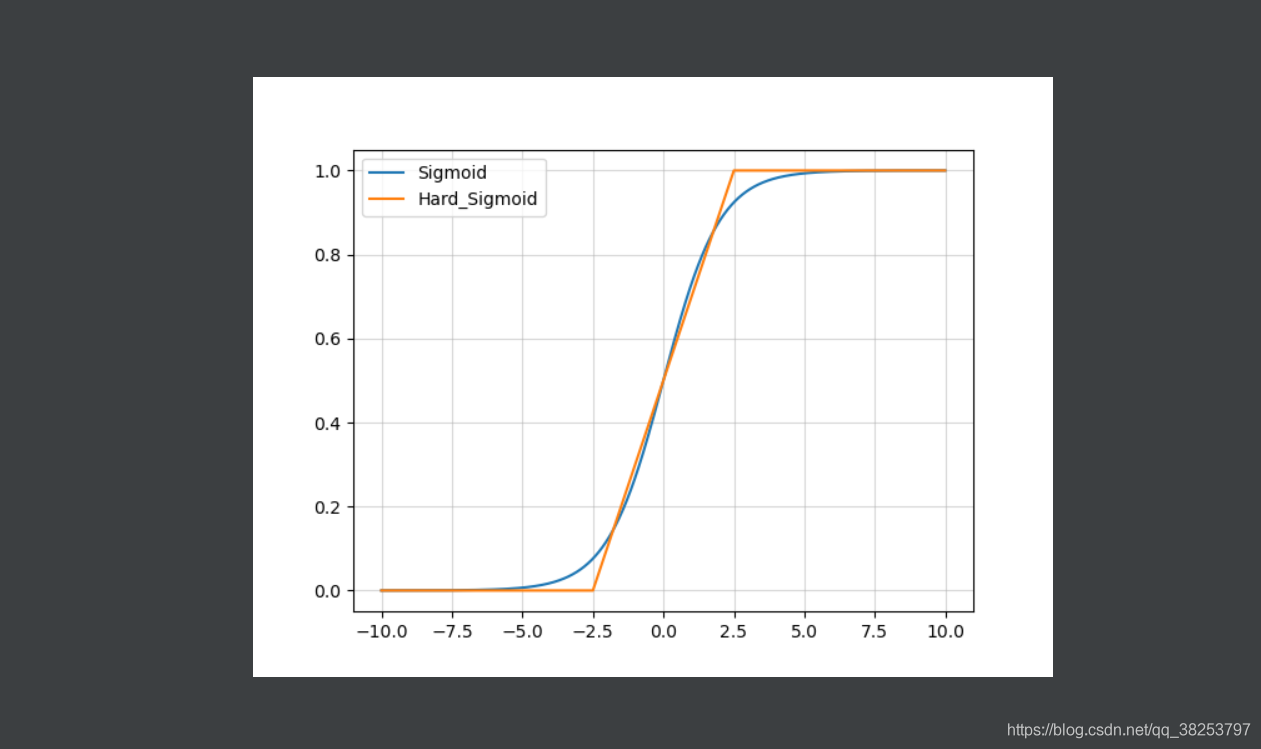
hard-Sigmoid函数图像及其导数图像:
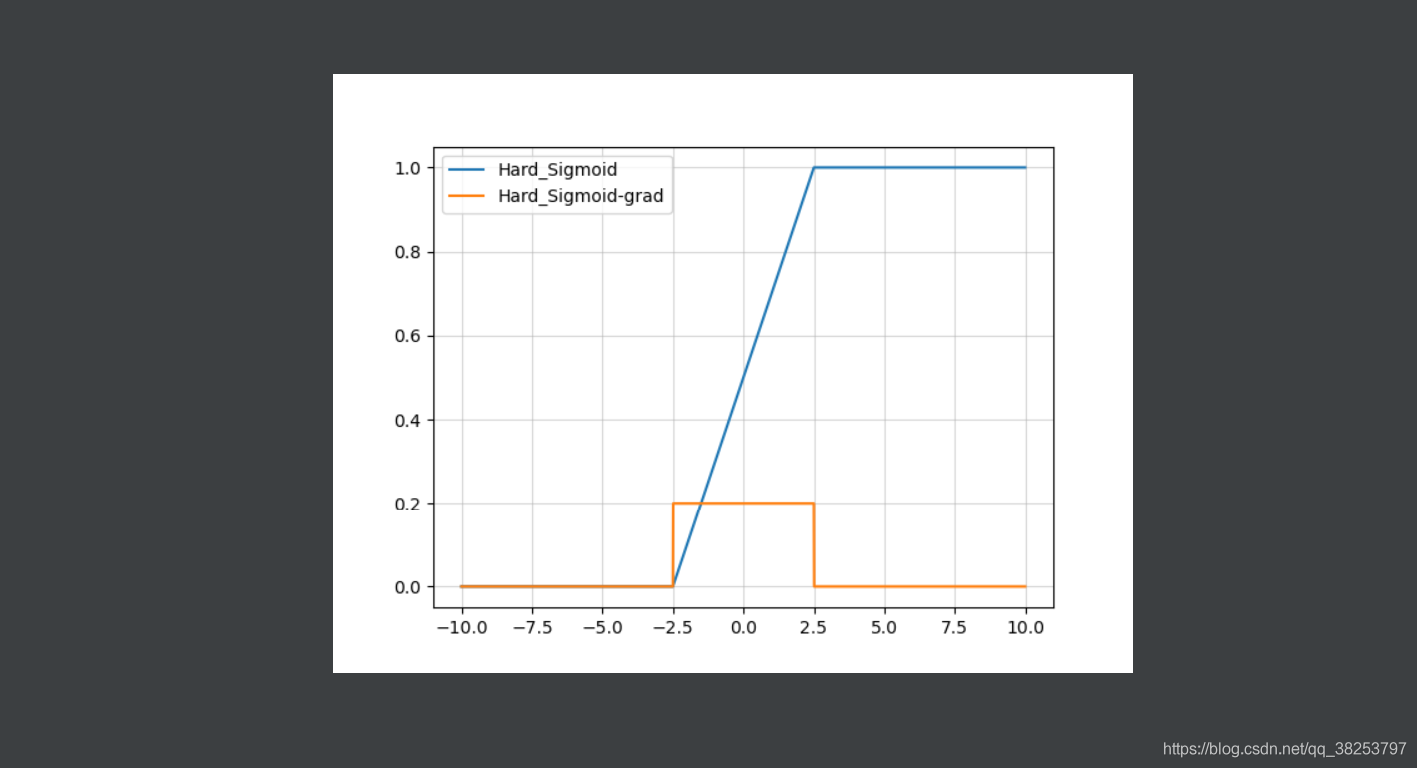
优点:
缺点:
函数表达式:

Tanh函数图像及其导函数图像:
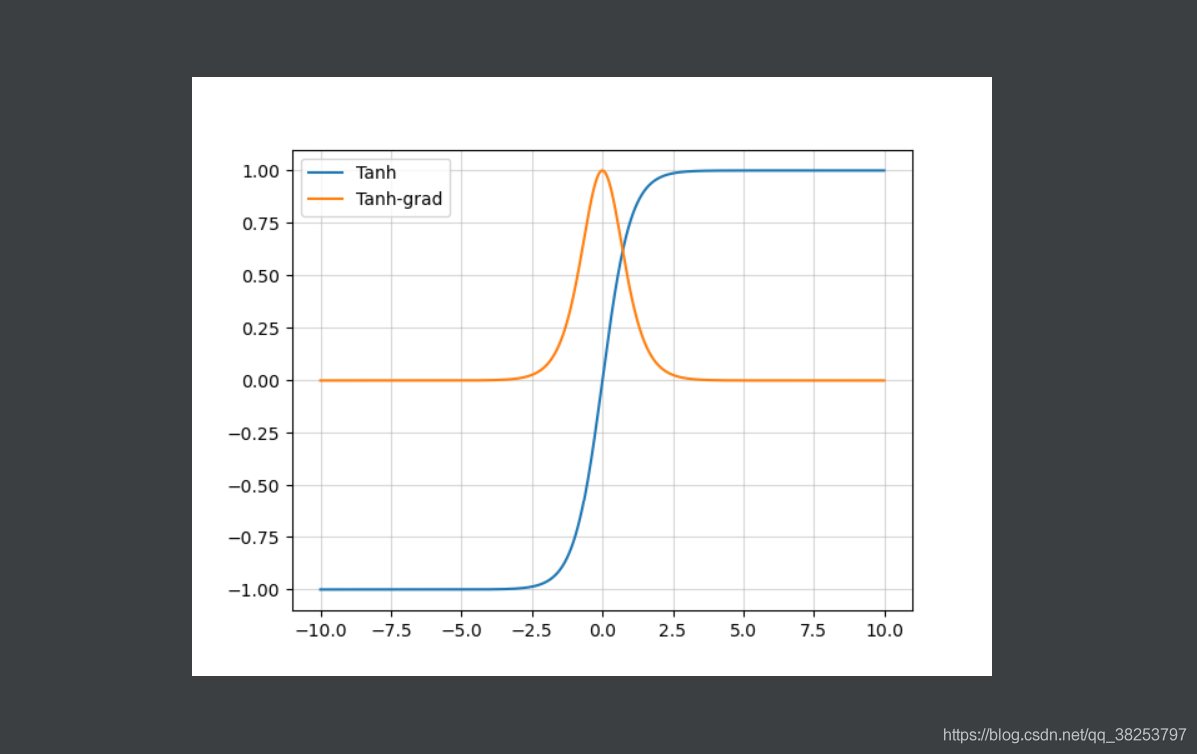
优点:
缺点:
函数表达式:
ReLU函数图像及其导数图像:
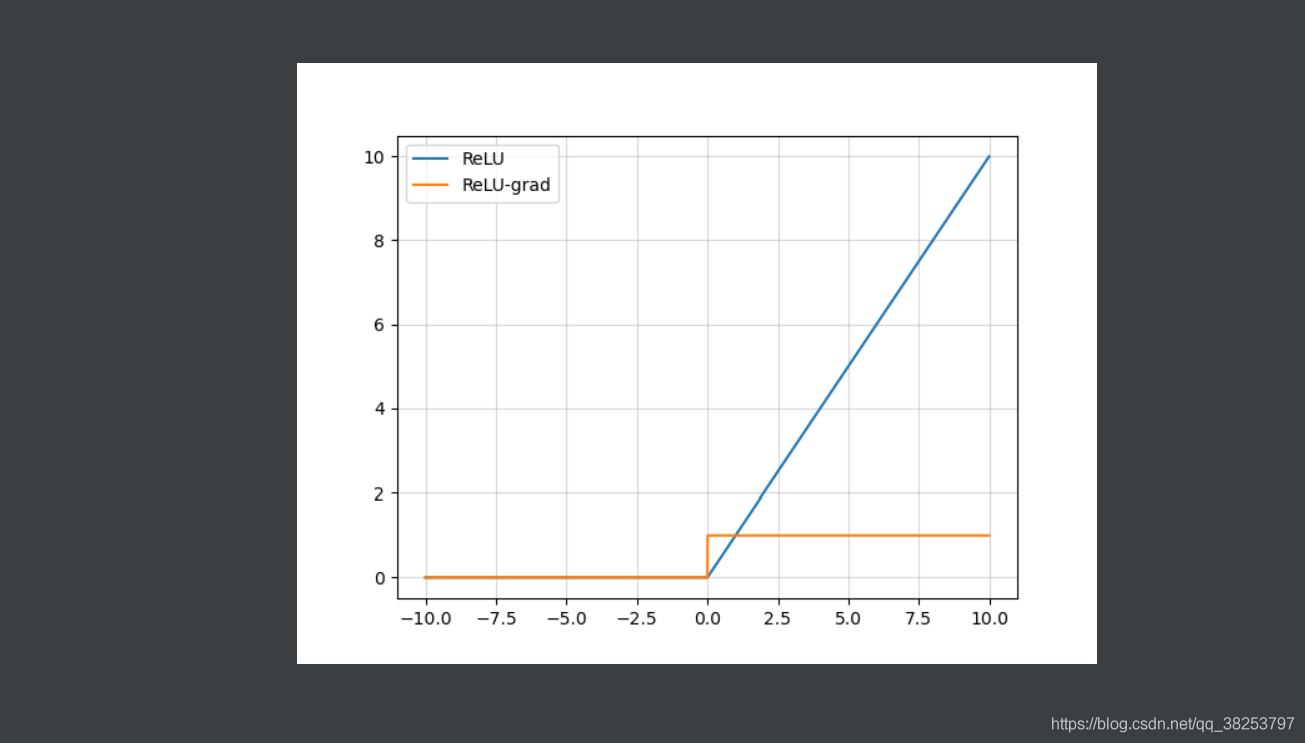
优点:
缺点:
函数表达式:

ReLU函数图像和ReLU6函数图像对比:
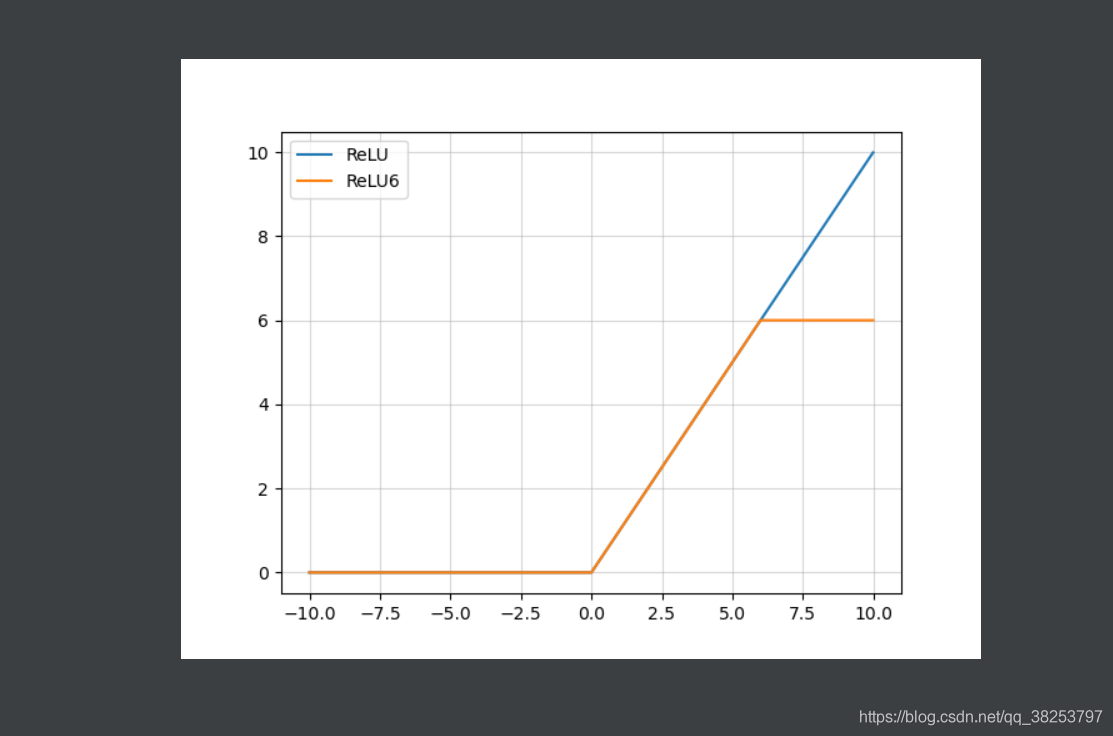
ReLU6函数图像及其导数图像:
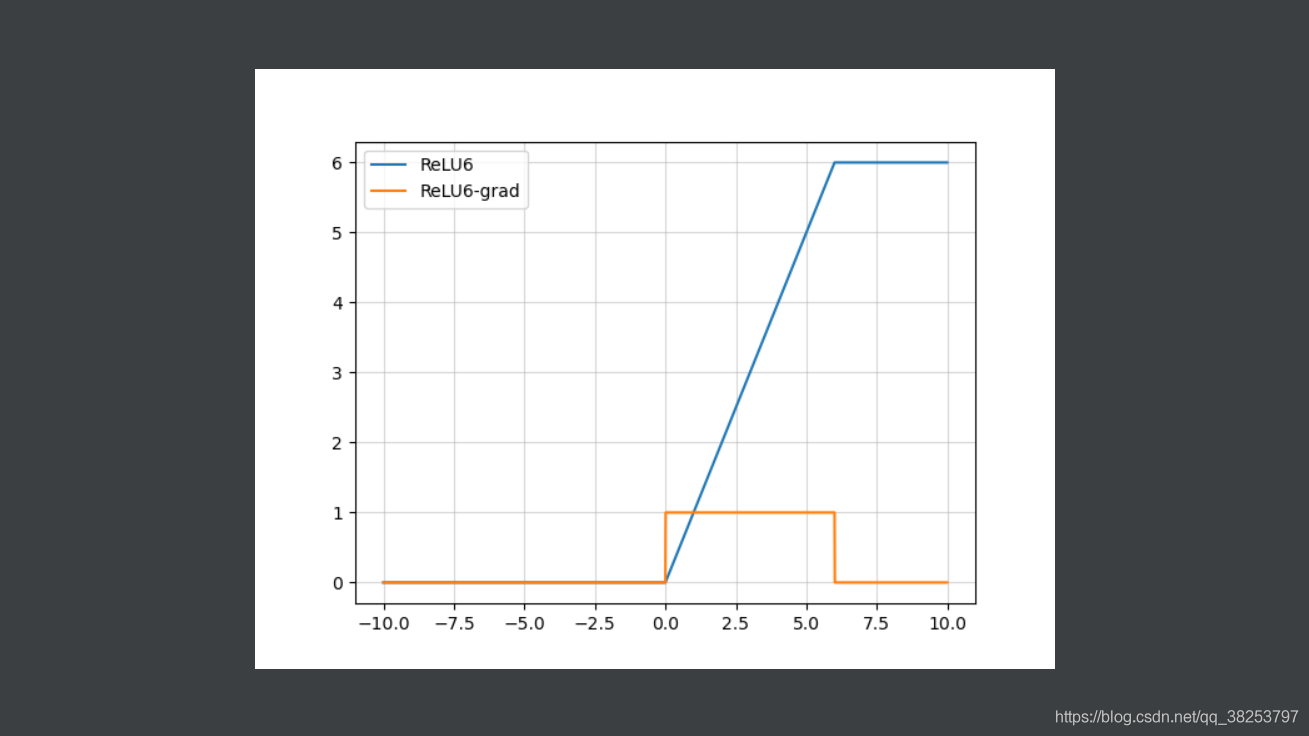
函数表达式:

ReLU函数图像和Leakly ReLU函数图像对比:
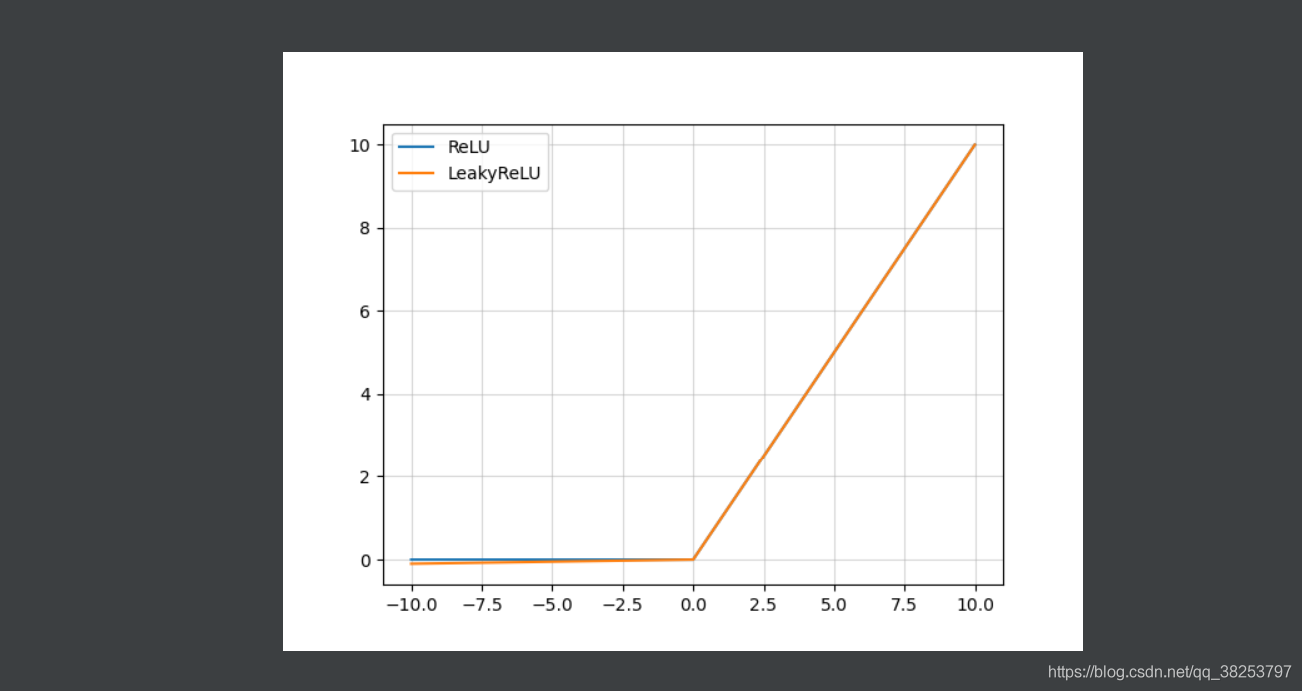
Leakly ReLU函数图像及其导数图像:
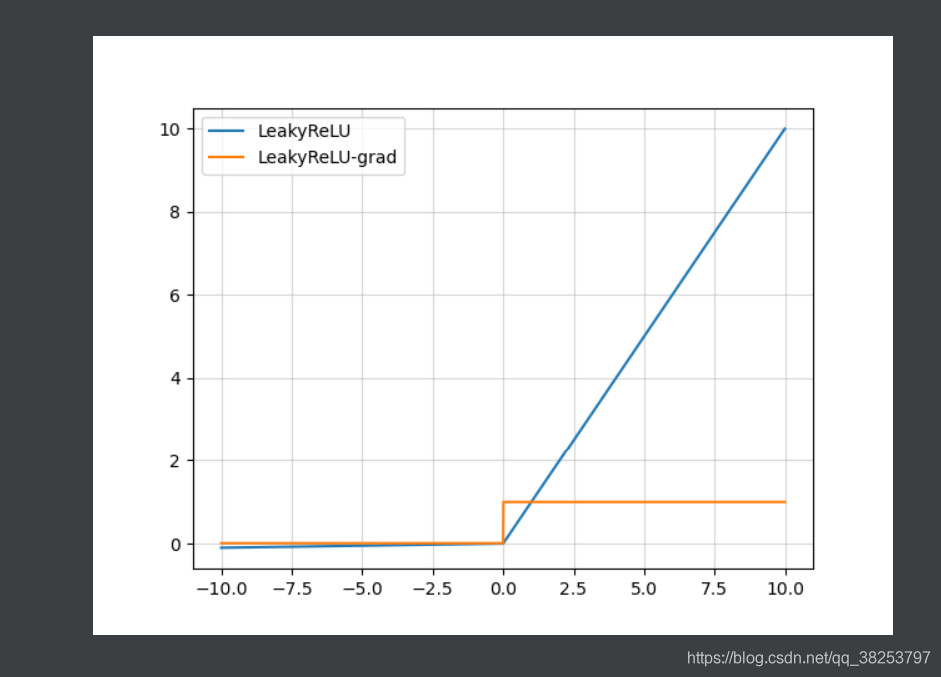
优点:
理论上Leaky ReLU 是优于ReLU的,但是实际操作中,并不一定。
函数公式:

注意:

函数图像:
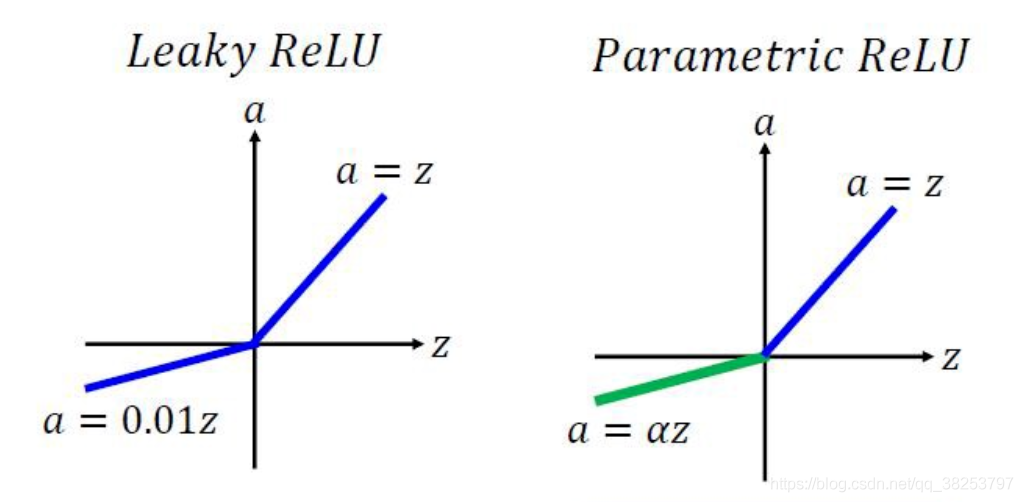
优点:
函数表达式:

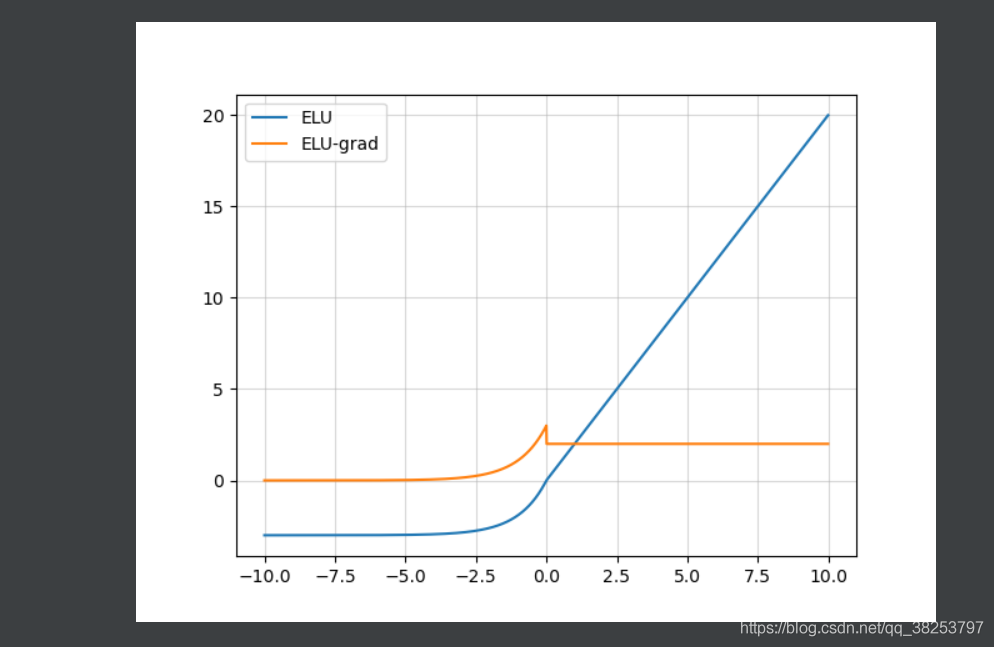
ELU函数图像及其导数图像( α = 1.5 \alpha=1.5 α=1.5):
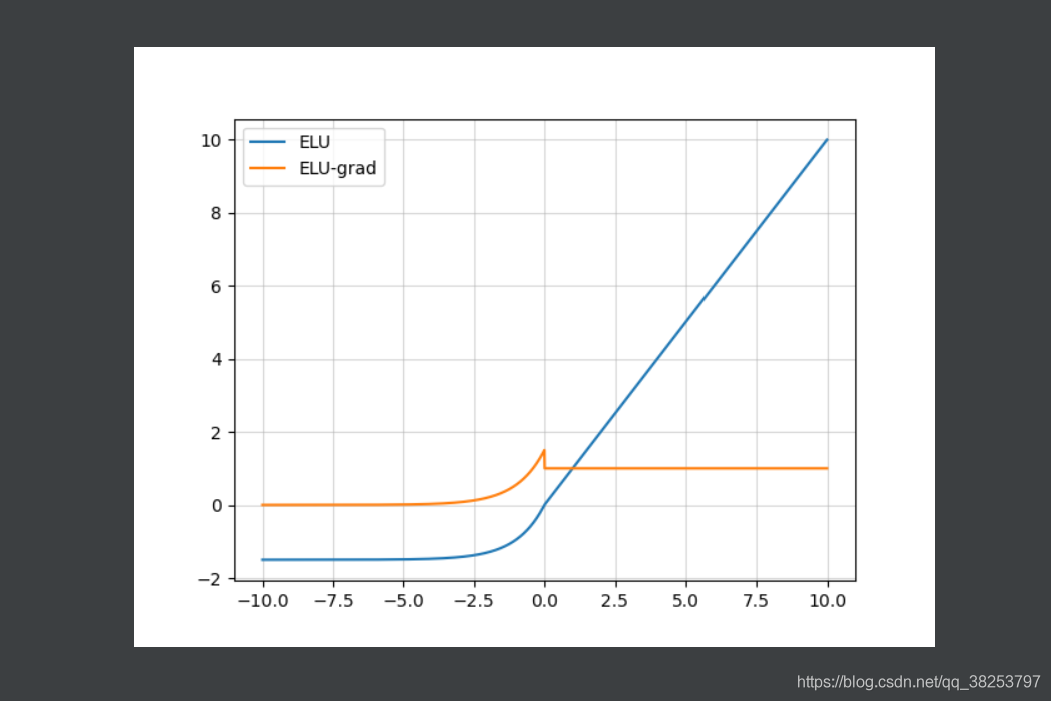
优点:
缺点:
理论上ELU优于ReLU, 但是真实数据下,并不一定。
SELU就是在ELU的基础上添加了一个 λ \lambda λ参数,且 λ > 1 \lambda>1 λ>1
函数表达式:

ELU函数图像和SELU函数图像对比( α = 1.5 , λ = 2 \alpha=1.5, \lambda=2 α=1.5,λ=2):
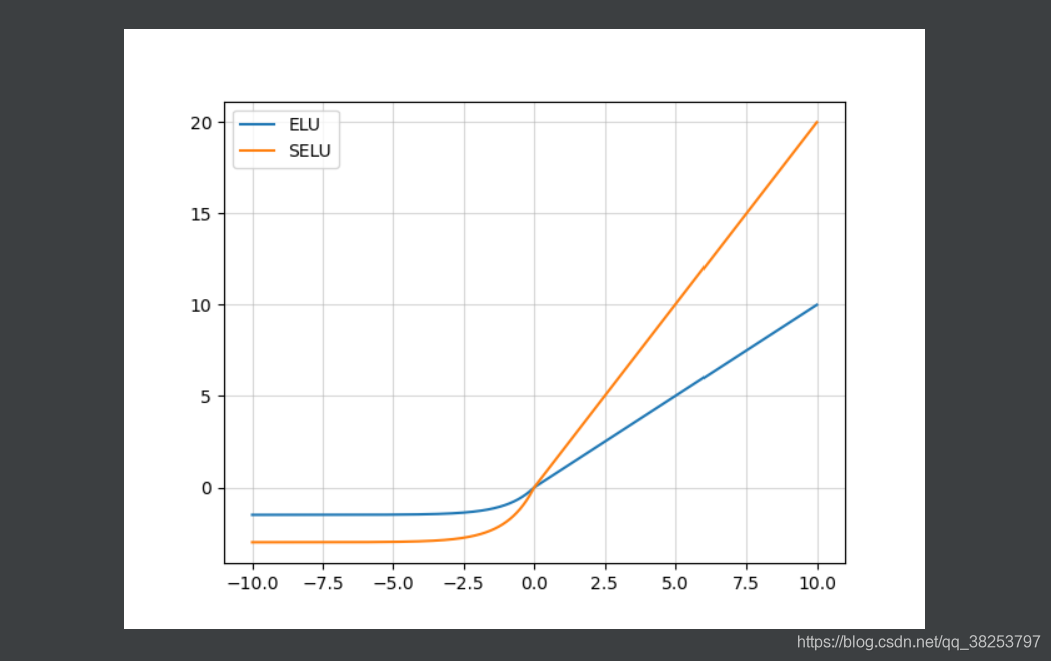
SELU函数图像及其导数图像( α = 1.5 , λ = 2 \alpha=1.5, \lambda=2 α=1.5,λ=2):
优点:
函数表达式:

Swish函数图像( β = 0.1 , β = 1 , β = 10 \beta=0.1, \beta=1,\beta=10 β=0.1,β=1,β=10):
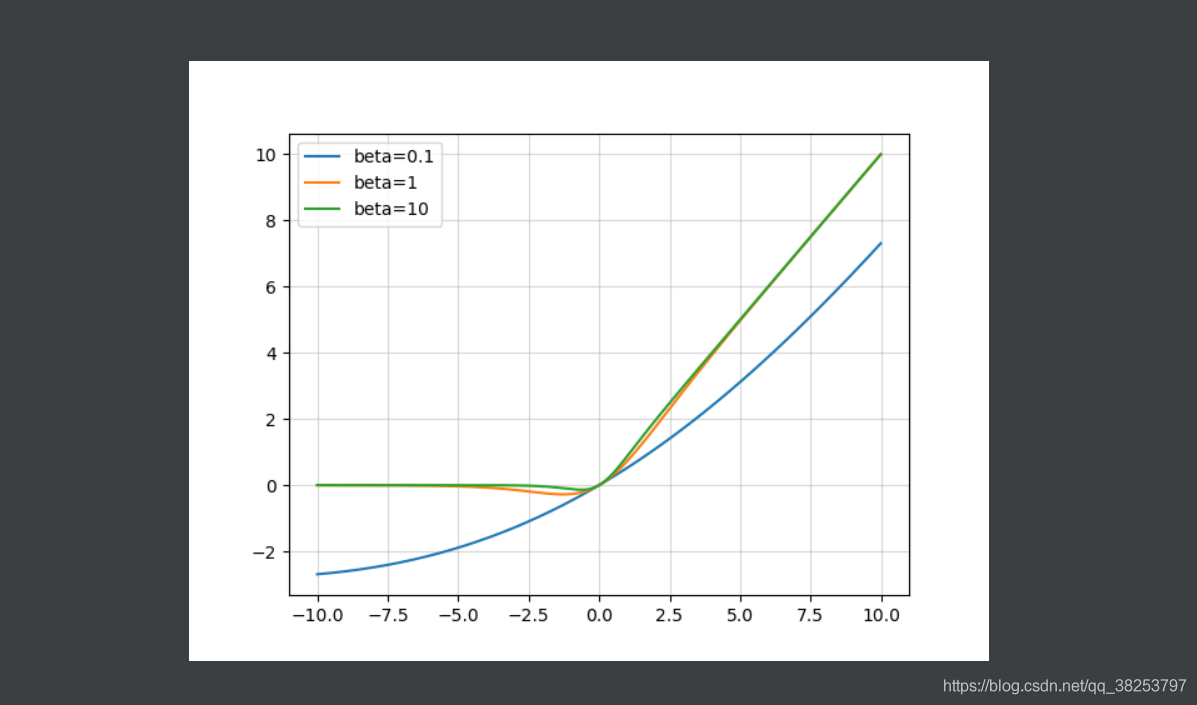
Swish函数梯度图像( β = 0.1 , β = 1 , β = 10 \beta=0.1, \beta=1,\beta=10 β=0.1,β=1,β=10):
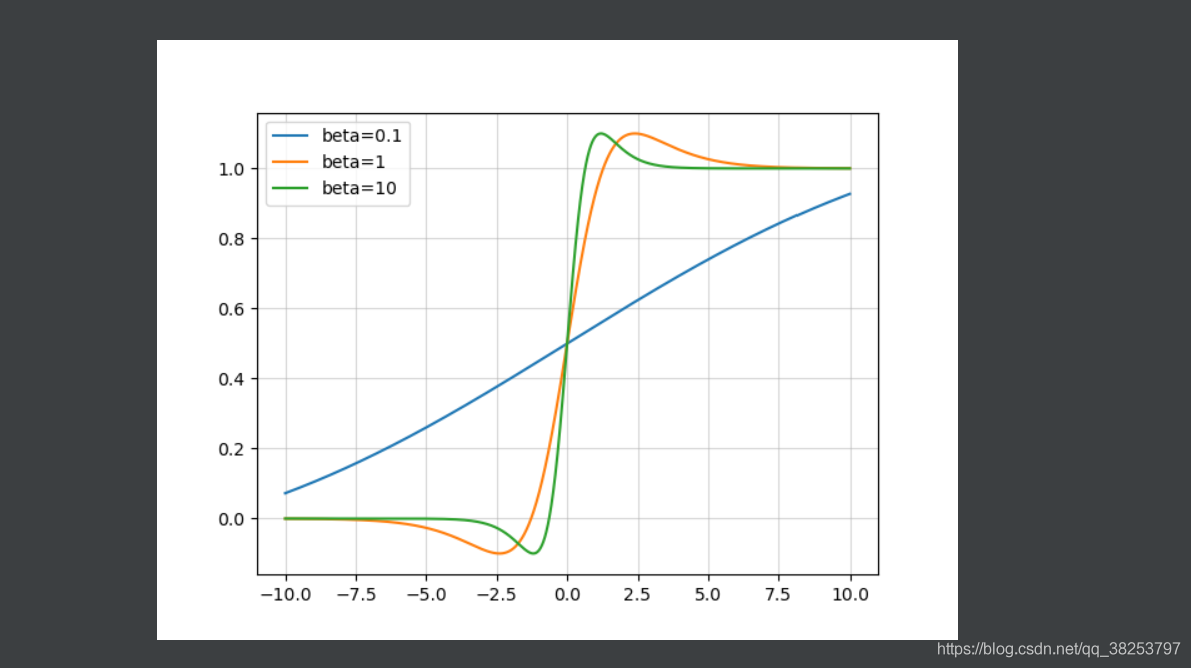
优点:
缺点:
hard = 硬,就是让图像在整体上没那么光滑(从下面两个图都可以看出来)
函数表达式:

hard-Swish函数图像和Swish( β = 1 \beta=1 β=1)函数图像对比:
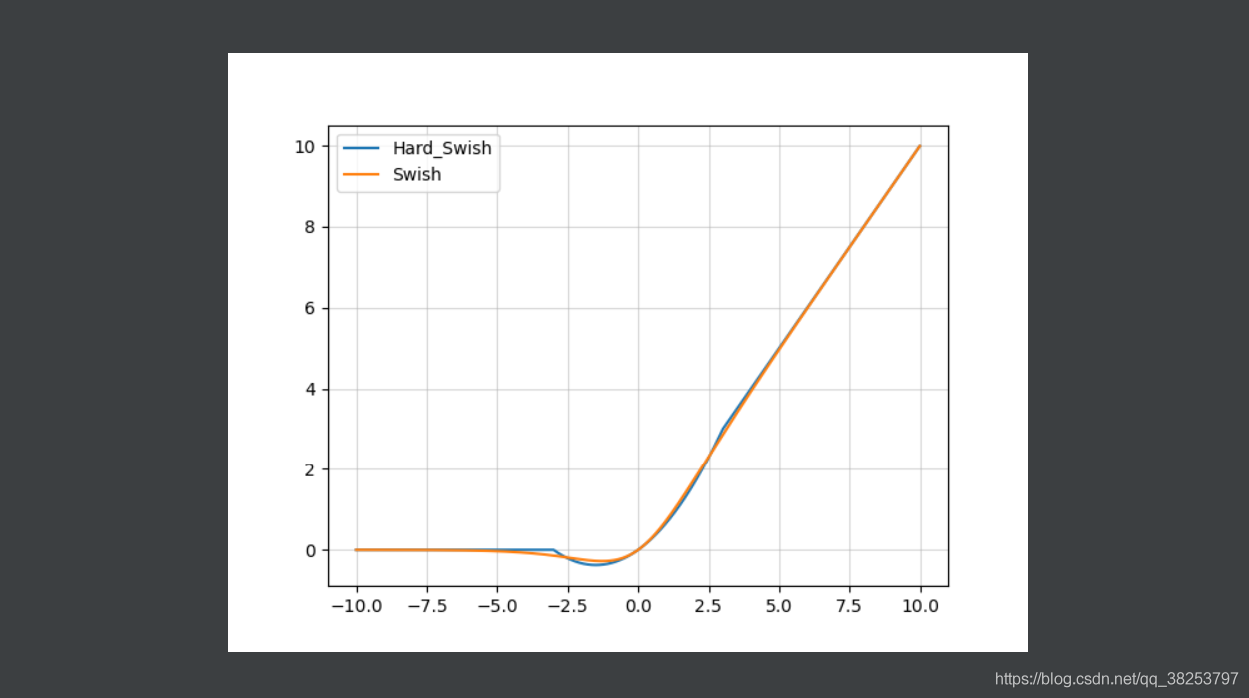
hard-Swish函数图像和Swish( β = 1 \beta=1 β=1)函数梯度图像对比:
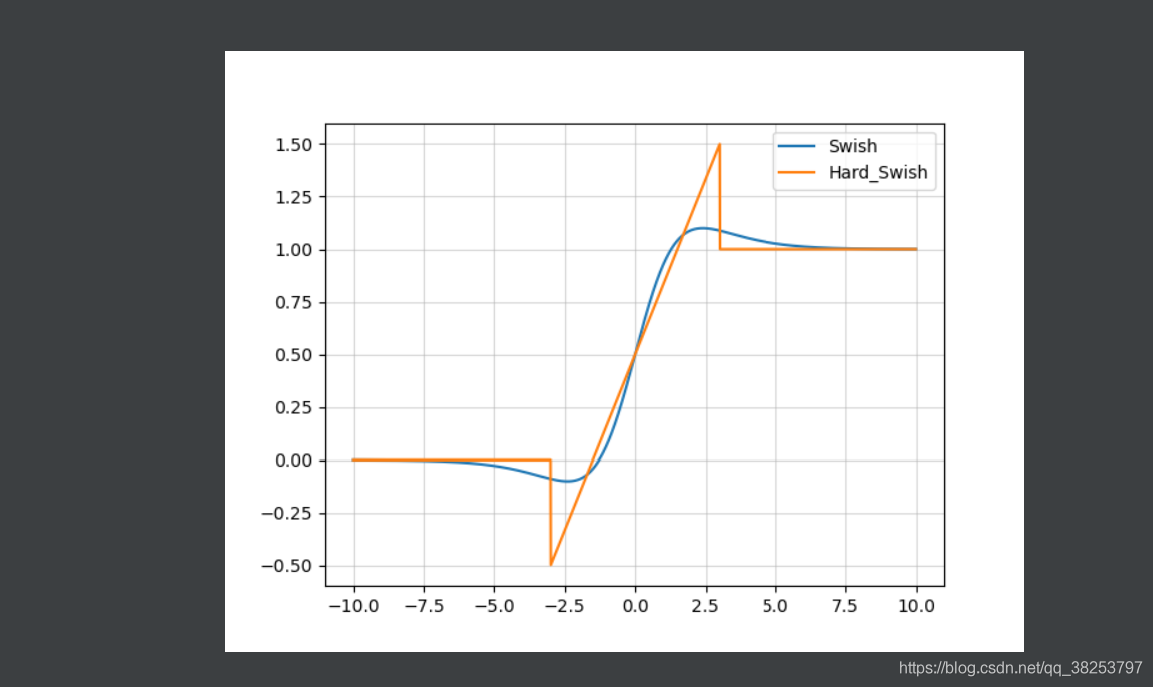
优点:
论文地址:
https://arxiv.org/pdf/1908.08681.pdf
关于激活函数改进的最新一篇文章,且被广泛用于YOLO4中,相比Swish有0.494%的提升,相比ReLU有1.671%的提升。
Mish函数公式:

Mish函数图像和Swish( β = 1 \beta=1 β=1)函数图像对比:
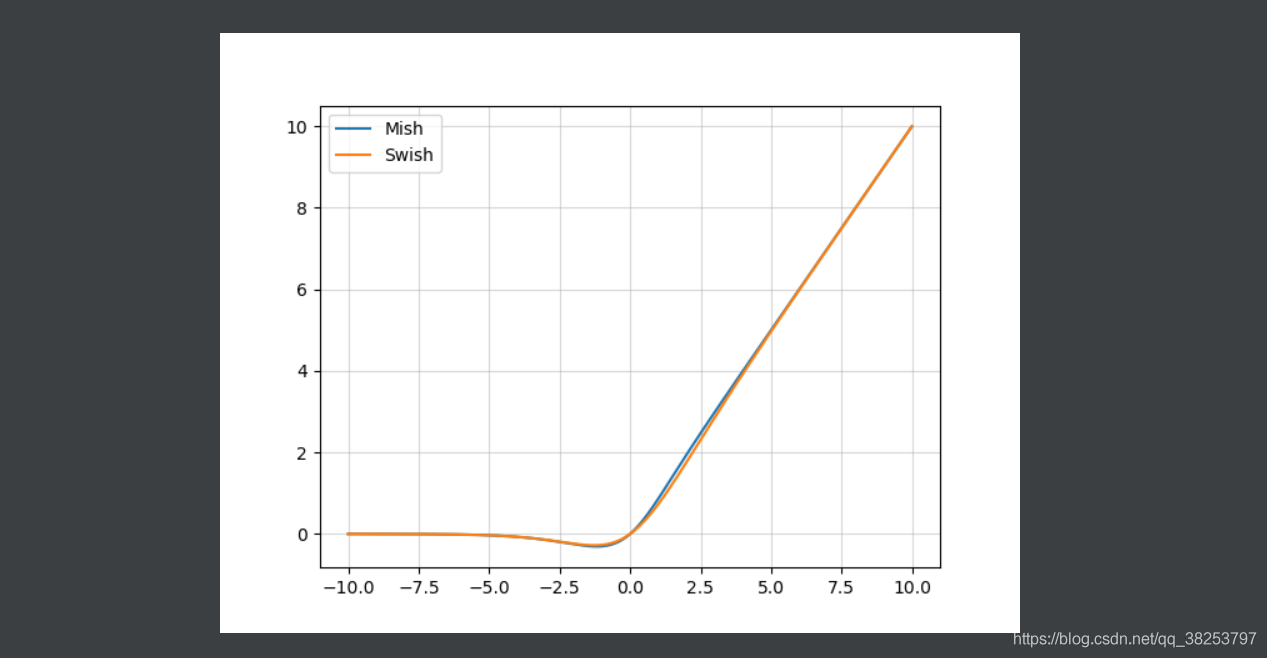
Mish函数图像和Swish( β = 1 \beta=1 β=1)函数导数图像对比:
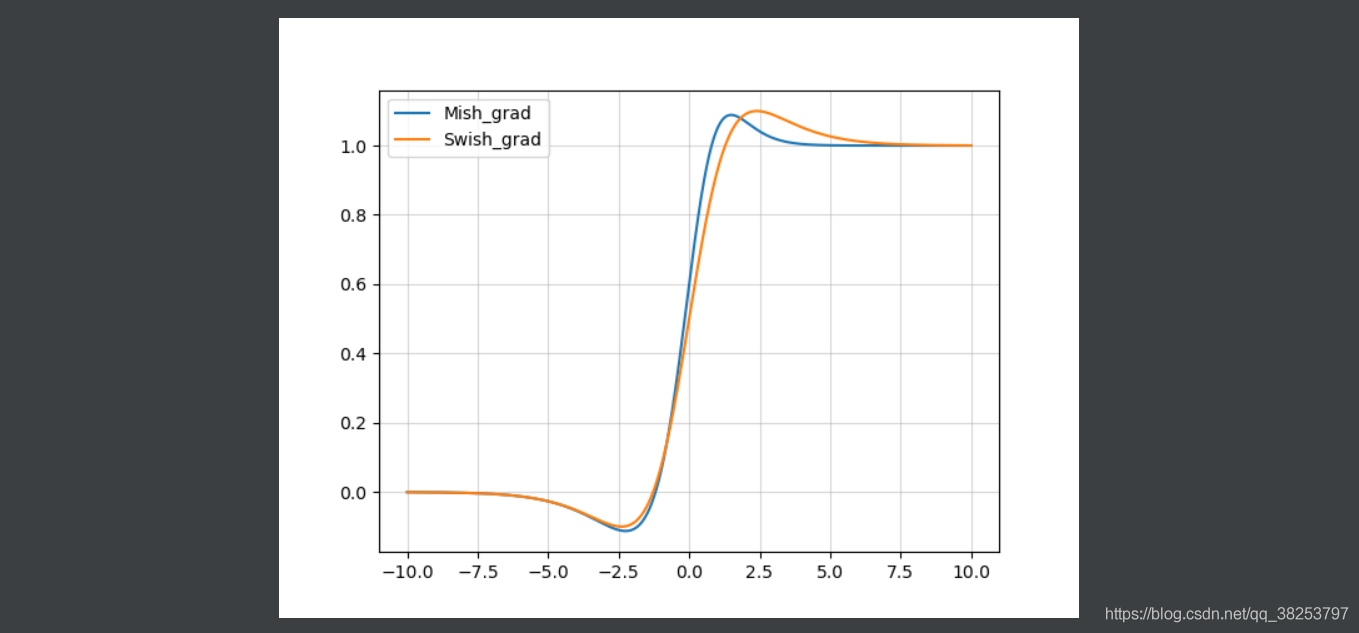
为什么Mish表现的更好:
上面无边界(即正值可以达到任何高度)避免了由于封顶而导致的饱和。理论上对负值的轻微允许更好的梯度流,而不是像ReLU中那样的硬零边界。
最后,可能也是最重要的,目前的想法是,平滑的激活函数允许更好的信息深入神经网络,从而得到更好的准确性和泛化。Mish函数在曲线上几乎所有点上都极其平滑。
import matplotlib.pyplot as plt
import numpy as np
class ActivateFunc():
def __init__(self, x, b=None, lamb=None, alpha=None, a=None):
super(ActivateFunc, self).__init__()
self.x = x
self.b = b
self.lamb = lamb
self.alpha = alpha
self.a = a
def Sigmoid(self):
y = np.exp(self.x) / (np.exp(self.x) + 1)
y_grad = y*(1-y)
return [y, y_grad]
def Hard_Sigmoid(self):
f = (2 * self.x + 5) / 10
y = np.where(np.where(f > 1, 1, f) < 0, 0, np.where(f > 1, 1, f))
y_grad = np.where(f > 0, np.where(f >= 1, 0, 1 / 5), 0)
return [y, y_grad]
def Tanh(self):
y = np.tanh(self.x)
y_grad = 1 - y * y
return [y, y_grad]
def ReLU(self):
y = np.where(self.x < 0, 0, self.x)
y_grad = np.where(self.x < 0, 0, 1)
return [y, y_grad]
def ReLU6(self):
y = np.where(np.where(self.x < 0, 0, self.x) > 6, 6, np.where(self.x < 0, 0, self.x))
y_grad = np.where(self.x > 6, 0, np.where(self.x < 0, 0, 1))
return [y, y_grad]
def LeakyReLU(self): # a大于1,指定a
y = np.where(self.x < 0, self.x / self.a, self.x)
y_grad = np.where(self.x < 0, 1 / self.a, 1)
return [y, y_grad]
def PReLU(self): # a大于1,指定a
y = np.where(self.x < 0, self.x / self.a, self.x)
y_grad = np.where(self.x < 0, 1 / self.a, 1)
return [y, y_grad]
def ELU(self): # alpha是个常数,指定alpha
y = np.where(self.x > 0, self.x, self.alpha * (np.exp(self.x) - 1))
y_grad = np.where(self.x > 0, 1, self.alpha * np.exp(self.x))
return [y, y_grad]
def SELU(self): # lamb大于1,指定lamb和alpha
y = np.where(self.x > 0, self.lamb * self.x, self.lamb * self.alpha * (np.exp(self.x) - 1))
y_grad = np.where(self.x > 0, self.lamb * 1, self.lamb * self.alpha * np.exp(self.x))
return [y, y_grad]
def Swish(self): # b是一个常数,指定b
y = self.x * (np.exp(self.b*self.x) / (np.exp(self.b*self.x) + 1))
y_grad = np.exp(self.b*self.x)/(1+np.exp(self.b*self.x)) + self.x * (self.b*np.exp(self.b*self.x) / ((1+np.exp(self.b*self.x))*(1+np.exp(self.b*self.x))))
return [y, y_grad]
def Hard_Swish(self):
f = self.x + 3
relu6 = np.where(np.where(f < 0, 0, f) > 6, 6, np.where(f < 0, 0, f))
relu6_grad = np.where(f > 6, 0, np.where(f < 0, 0, 1))
y = self.x * relu6 / 6
y_grad = relu6 / 6 + self.x * relu6_grad / 6
return [y, y_grad]
def Mish(self):
f = 1 + np.exp(x)
y = self.x * ((f*f-1) / (f*f+1))
y_grad = (f*f-1) / (f*f+1) + self.x*(4*f*(f-1)) / ((f*f+1)*(f*f+1))
return [y, y_grad]
def PlotActiFunc(x, y, title):
plt.grid(which='minor', alpha=0.2)
plt.grid(which='major', alpha=0.5)
plt.plot(x, y)
plt.title(title)
plt.show()
def PlotMultiFunc(x, y):
plt.grid(which='minor', alpha=0.2)
plt.grid(which='major', alpha=0.5)
plt.plot(x, y)
if __name__ == '__main__':
x = np.arange(-10, 10, 0.01)
activateFunc = ActivateFunc(x)
activateFunc.a = 100
activateFunc.b= 1
activateFunc.alpha = 1.5
activateFunc.lamb = 2
plt.figure(1)
PlotMultiFunc(x, activateFunc.Sigmoid()[0])
PlotMultiFunc(x, activateFunc.Hard_Sigmoid()[0])
PlotMultiFunc(x, activateFunc.Tanh()[0])
PlotMultiFunc(x, activateFunc.ReLU()[0])
PlotMultiFunc(x, activateFunc.ReLU6()[0])
PlotMultiFunc(x, activateFunc.LeakyReLU()[0])
PlotMultiFunc(x, activateFunc.ELU()[0])
PlotMultiFunc(x, activateFunc.SELU()[0])
PlotMultiFunc(x, activateFunc.Swish()[0])
PlotMultiFunc(x, activateFunc.Hard_Swish()[0])
PlotMultiFunc(x, activateFunc.Mish()[0])
plt.legend(['Sigmoid', 'Hard_Sigmoid', 'Tanh', 'ReLU', 'ReLU6', 'LeakyReLU',
'ELU', 'SELU', 'Swish', 'Hard_Swish', 'Mish'])
plt.show()
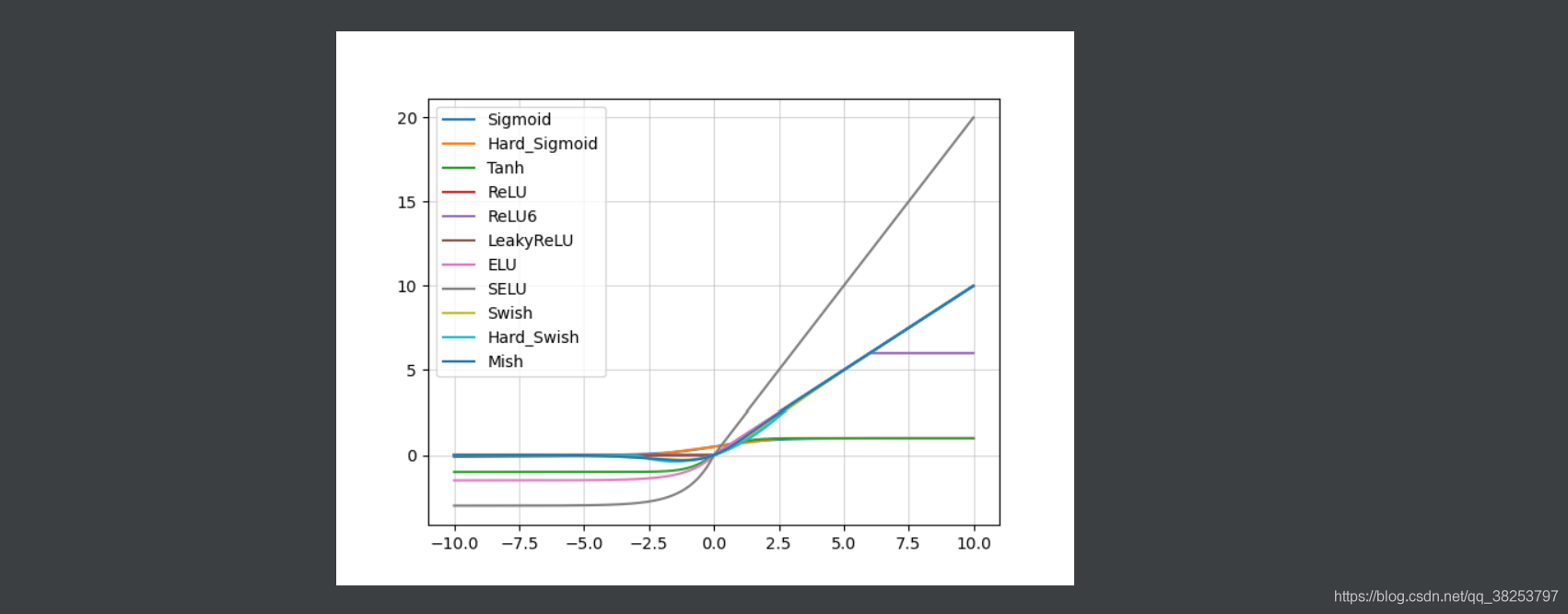
Reference
https://arxiv.org/pdf/1908.08681.pdf