之前讲过背包问题,线性DP,区间DP,不知道大家忘了吗,这次是计数类DP
老规矩,先画图。
思路:把1,2,3, … n分别看做n个物体的体积,这n个物体均无使用次数限制,问恰好能装满总体积为n的背包的总方案数(完全背包问题变形)
初值问题:
求最大值时,当都不选时,价值显然是 0
而求方案数时,当都不选时,方案数是 1(即前 i 个物品都不选的情况也是一种方案),所以需要初始化为 1
即:for (int i = 0; i <= n; i ++) f[i][0] = 1;
等价变形后: f[0] = 1
状态计算:
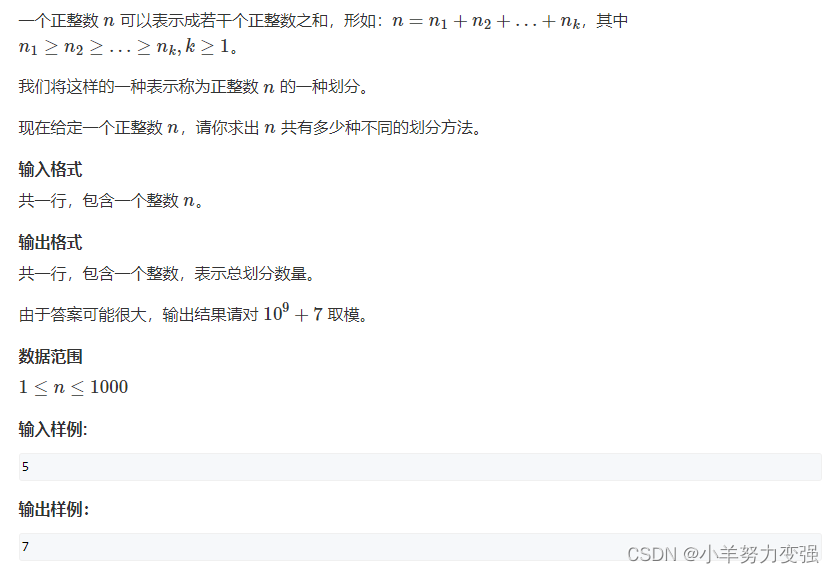
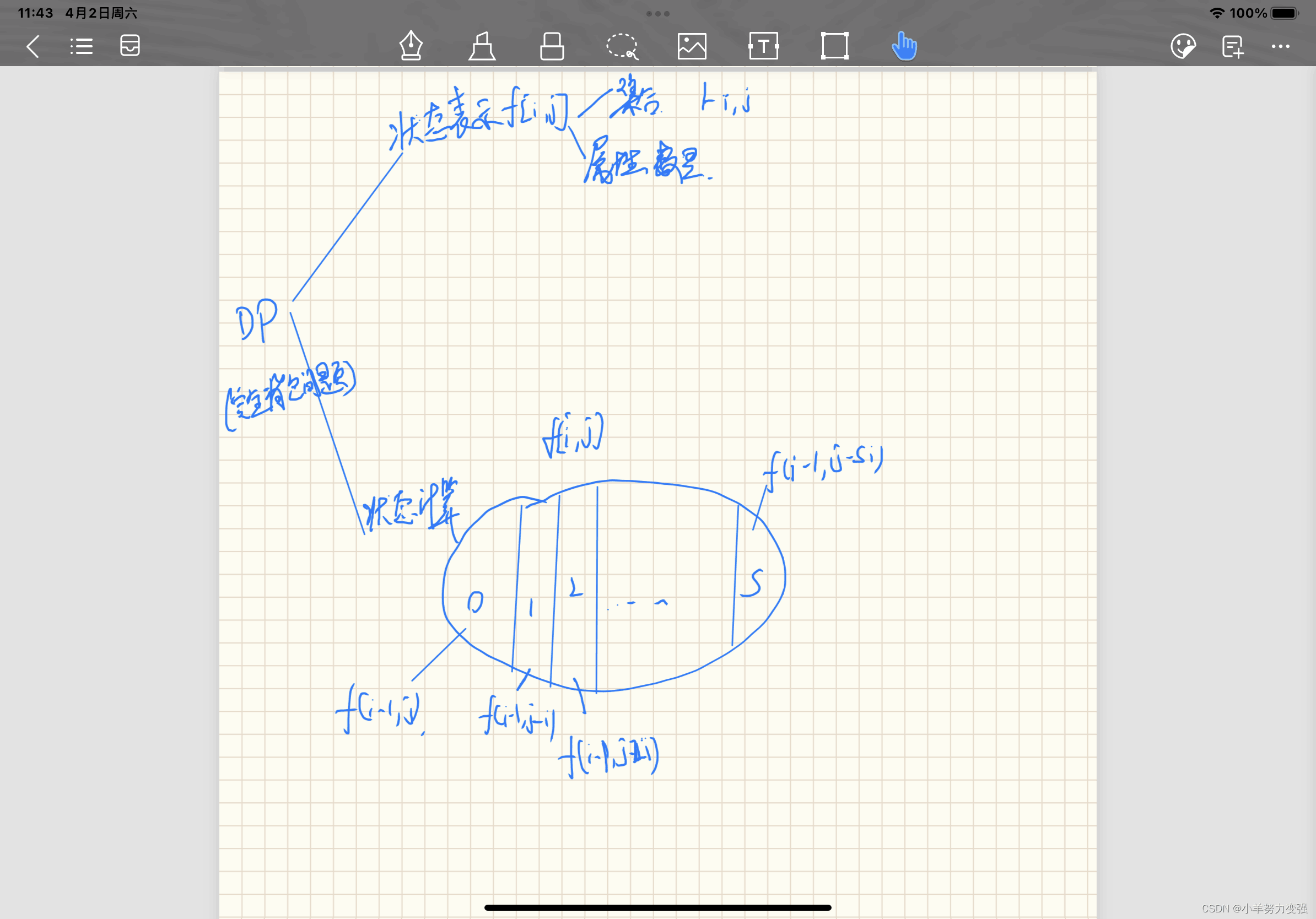
f[i][j]表示前i个整数(1,2…,i)恰好拼成j的方案数
求方案数:把集合选0个i,1个i,2个i,…全部加起来
f[i][j] = f[i - 1][j] + f[i - 1][j - i] + f[i - 1][j - 2 * i] + …;
f[i][j - i] = f[i - 1][j - i] + f[i - 1][j - 2 * i] + …;
因此 f[i][j]=f[i−1][j]+f[i][j−i]; (这一步类似完全背包的推导)
朴素做法
// f[i][j] = f[i - 1][j] + f[i][j - i]
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 7, mod = 1e9 + 7;
int f[N][N];
int main() {
int n;
cin >> n;
for (int i = 0; i <= n; i ++) {
f[i][0] = 1; // 容量为0时,前 i 个物品全不选也是一种方案
}
for (int i = 1; i <= n; i ++) {
for (int j = 0; j <= n; j ++) {
f[i][j] = f[i - 1][j] % mod; // 特殊 f[0][0] = 1
if (j >= i) f[i][j] = (f[i - 1][j] + f[i][j - i]) % mod;
}
}
cout << f[n][n] << endl;
}
等价变形
// f[i][j] = f[i - 1][j] + f[i][j - i]
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 7, mod = 1e9 + 7;
int f[N];
int main() {
int n;
cin >> n;
f[0] = 1; // 容量为0时,前 i 个物品全不选也是一种方案
for (int i = 1; i <= n; i ++) {
for (int j = i; j <= n; j ++) {
f[j] = (f[j] + f[j - i]) % mod;
}
}
cout << f[n] << endl;
}
上面是完全背包问题的解法,再来看看不用完全背包问题求解
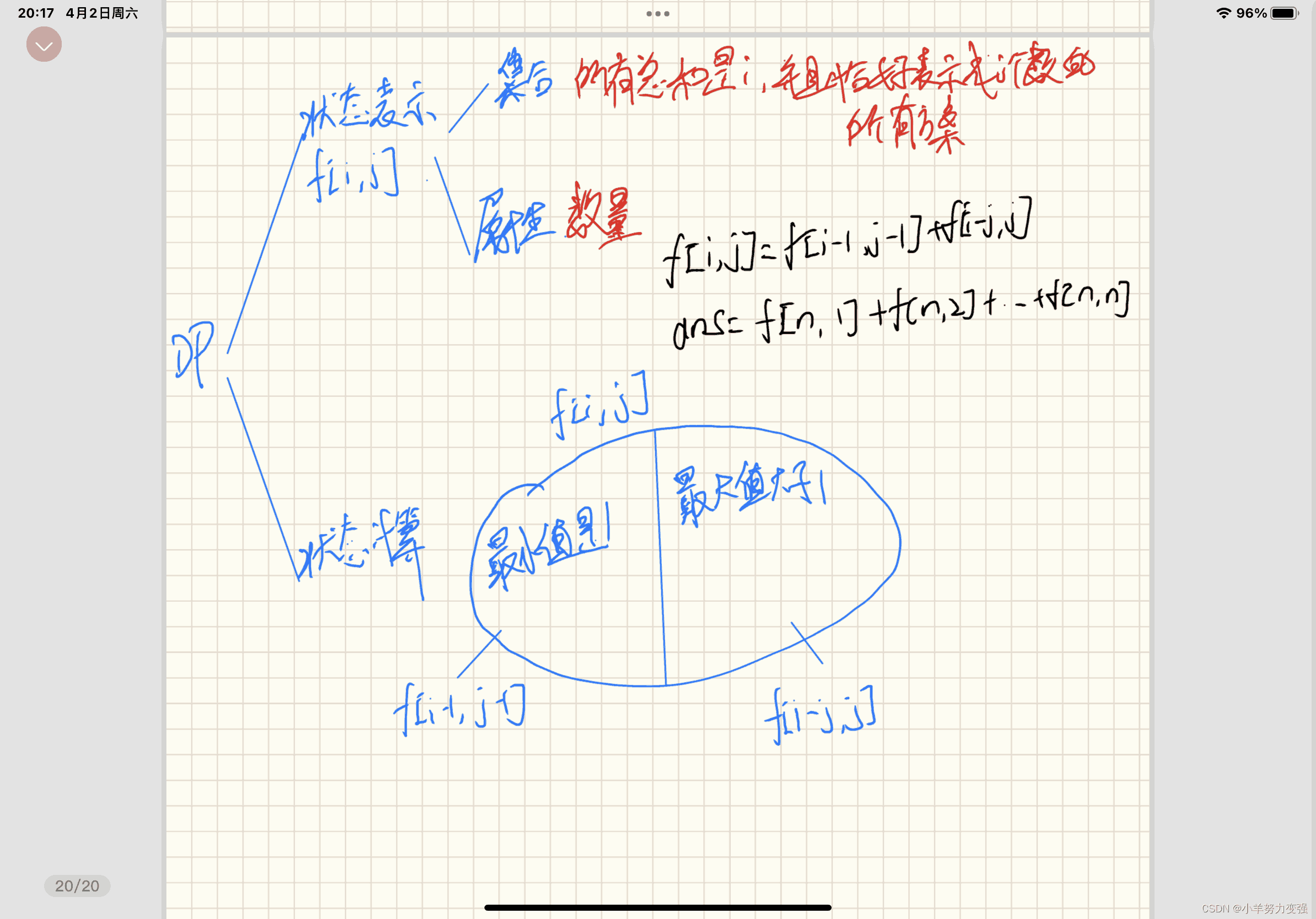
状态计算:分两部分
综上所述:f[i][j] = f[i - 1][j - 1] + f[i - j][j];
//非背包做法
//状态表示:f[i][j] 所有总和是i,并且恰好可以表示成j个数的和的方案
#include <bits/stdc++.h>
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int n;
int f[N][N];
int main()
{
cin >> n;
f[0][0] = 1;
for (int i = 1; i <= n; i ++ )
//i最多表示成i个数的和,因此j<=i
for (int j = 1; j <= i; j ++ )
f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % mod;
int res = 0;
for (int i = 1; i <= n; i ++ ) res = (res + f[n][i]) % mod;
cout << res << endl;
return 0;
}