浮点数在内存的存储方式为:符号位,指数,尾数
| 类型 | 符号位 | 指数 | 尾数 |
| float | 1位(第31位) | 8位(第23--30位) | 23位(第0--22位) |
| double | 1位(第63位) | 11位(第52--62位) | 52位(第0--51位) |
注:float 与 double 类型的数据在计算机内部的表示法是相同的,但由于所占存储空间的不同,其分别能够表示的数值范围和精度不同。
浮点数的转换
注意:计算指数时需要加上偏移量,而偏移量的值与类型有关。
示例:对于指数6,偏移后的值如下:
float:127 + 6 -> 133
double:1023 + 6-> 1029
实数 8.25 的在内存中的 float 表示
8.25的二进制表示:1000.01 -> 1.00001 * (2 ^ 3)
内存中 8.25 的 float 表示:
下面看一下 8.25 是不是在内存中表示为 0x41040000 吧:
#include <stdio.h>
int main()
{
float f = 8.25;
unsigned int* p = (unsigned int*)&f;
printf("0x%08X\n", *p);
return 0;
}下面为输出结果:
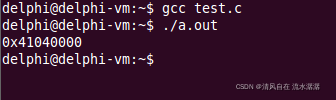
首先看一下 int 类型和 float 类型的范围:
int 类型的范围:[-2 ^ 31,2 ^ 31 - 1]
float 类型的范围:[-3.4 * 10 ^ 38,3.4 * 10 ^ 38]
这就出现一个问题:int 和 float 都占4个字节的内存,为什么 float 却比 int 的范围大得多呢?
解释如下:
注意:double 与 float 具有相同的内存表示法,因此 double 也是不精确的。由于 double 占用的内存较多,所能表示的精度比 float 高。
下面看一段 float 类型的不精确示例代码:
#include <stdio.h>
int main()
{
float f = 3.1415f;
float fl = 123456789;
printf("%0.10f\n", f);
printf("%0.10f\n", fl);
return 0;
}下面为输出结果:
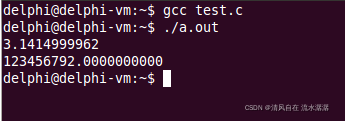
这个示例就是表示 f 和 fl 小数点的后 10 位,结果表明,float 只是一种近似的表示法,不能作为精确数使用以及float 可表示的数字之间不是连续的,存在间隙。